Numerical Simulation of Particle Trajectories in Ion Thruster Grid Region Plasma using a PIC-DSMC Code

There are many types of propulsion systems used in space applications. The most general category is liquid-fueled high-thrust rocket engines used during the mission's ascent phase. Generally, these engines fire for around 100-120 seconds with extremely high amounts of thrust. Another category is electrified propulsion which uses ionized Xenon gas. Even though they have little thrust compared to their liquid-fueled counterparts, they become beneficial for their efficiency and precision during course correction burns. Long space missions using multiple gravity assists or communications satellites rely on them for their unique properties.

Some electric propulsion methods include pressure-feed thrust, where the pressure results from the repulsive electric force between ionized gas molecules. The type of system that we are interested in is ion thrusters. They generate plasma by exciting the initially neutral Xenon gas and accelerating it between anode and cathode grids, specifically screen and acceleration grids. High electric potential difference causes a strong electric field in this region. The grid region is the equivalent of the converging-diverging nozzle in liquid-fueled engines, except that there is an electric force rather than thermodynamic effects of compressible flow.

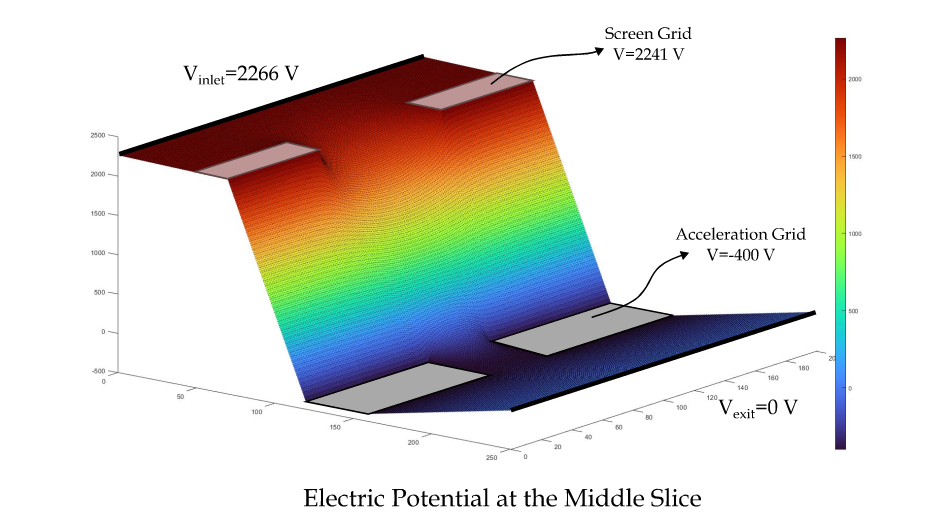
A custom finite element code is written in C++ to compute electric potential from Poisson's equation, derive the resultant electric field, create ion and neutral macroparticles, move them with electric force and apply collisions or reflections if necessary. PIC stands for *Particle in Cell* method in which the motion of the particles is executed continuously, but a weighting procedure is used to assign them to nearby mesh nodes to be able to solve the finite element equations. DSMC is acronym for *Direct Simulation Monte-Carlo*. In my opinion, it is a fancy way of saying probability:smile: However, it is advantageous when an analytical model will be computationally heavier. For our case, we use DSMC to find whether or not a collision has occurred, assignment of the initial velocity of ions using Maxwellian Velocity Distribution, and position assignment for particles to enter into the domain. Two types of solvers are used to extract electric potential at mesh nodes from discretized Poisson's equation. To optimize the code using the symmetries of the system, we only simulate the triangular prism volume and use cylindrical coordinates to construct equations. Neumann and Dirichlet boundary conditions are used to specify grid walls and boundaries of the simulation domain.

The last video may be misleading, but it is an aesthetically pleasing simulation. You can see the reflected wave later constructs a Mach diamond-like shape. At first, the reflection of ions from the screen grid was permitted, but as it turns out, just like the acceleration grid, the screen grid causes ions to lose their charge and reflect them as neutrals, too.